The Beatles’ Magical Mystery Chord
On the 16th April 1964 the Beatles, George Harrison, Paul McCartney, John Lennon and Ringo Starr, were on the cusp between stardom and mega-stardom. Groundbreaking albums, hit films, cartoons, royal honours, Sgt. Pepper, Indian mysticism, and an acrimonious break up all lay in their future as did the murder of Lennon and attempted murder of Harrison by separate mentally disturbed fans.
That was all to come. Their task that night was to record an impressive opening track for their forthcoming debut film and the album to accompany it. Their producer, George Martin, wanted something spectacular: ‘We were looking for something big to open it with, an introduction. It needed a strong chord, a dramatic thing’ (p487 of Dominic Pedler, The Songwriting Secrets of the Beatles, Omnibus Press, 2003).
Those present in the Abbey Road studio to record Lennon’s song A Hard Day’s Night could not have imagined that 50 years later the events would still be analyzed and dissected. Particularly since the focus of the analysis is almost not a piece of music, it’s a short sound, less than 3 seconds long, a crashing, ringing, chiming sound that has caused arguments and discussions between Beatles’ fans and musicologists ever since it was recorded.
The noise is impossible to describe accurately in words – the famous quote ‘writing about music is like dancing about architecture’ comes to mind. The sound can be heard here:
The central question is simple: What is it? That is, what notes are played and who is playing them? Many versions have been suggested. In his massive Beatles book, The Songwriting Secrets of the Beatles, Dominic Pedler collects twenty one educated guesses from various sources and devotes over 40 pages to discussion, including his own theory. It is not difficult to produce a chord that is close – strumming a guitar without fretting produces a similar sound. It’s close. But close is not exact, right? So, what is it really?
In 2004 a mathematician claimed to have discovered this musical holy grail by applying mathematics. Once and for all, the riddle was solved because, after all, mathematics is not wrong and you can’t beat the scientists with their fancy abstract toys. Except there was a problem. He got it horribly wrong.
Here, for the honour of all mathematicians, I would like to put the record straight — or at least straighter. The mathematical tale of the Beatles’ Magical Mystery Chord is a tale of 18th century mathematicians, the study of heat, Karaoke tricks and a measure of luck.
The quest begins
I am a mathematics lecturer who enjoys promoting mathematics to school children and the general public. My introduction to the mystery of the chord came not from a love of the Beatles music but a desire to show off in front of my parents. My mathematics promotion involves giving talks all over the country but as I live in the north of England and my parents live in a secluded part of the north east of Scotland, they would under normal circumstances be unable to see their second son on a stage explaining mathematics.
Back in 2011 I heard that the British Science Festival would be held the following year in Aberdeen which is close to where my parents live. The festival is held in a different city in the UK each year and aims to engage the general public in science. Hundreds of events take place over a week in September with debates, demonstrations and hands-on exhibitions at the local university as well as theatres and even, like maths busking, in the street. (Maths busking is as it sounds. Mathematicians go out in the street and do mathematics to entertain passers-by. I’ve tried it and it is hard. See my report here.)
All I had to do was offer to give a talk, get accepted and I would get my chance to impress my parents. My best talk involves the mathematics of card tricks but that subject was already a regular at the festival so that was out. My other talks weren’t suitable so I needed a new talk. I decided on the mathematics of Auto-Tune. This is a clever piece of software that allows out-of-tune singers to sound in-tune. The resulting talk I wrote on the mathematics of this was too short and if I’m honest a bit dry in that it didn’t have many good examples and stories.
To enliven the talk I searched for examples where mathematics and music come together. A good one appeared in an online article about the A Hard Day’s Night chord problem. A mathematician, Jason Brown of Dalhousie University, had used mathematics to unravel the chord. Great, I thought, a perfect example of how mathematics solves mysteries. I digested his article and incorporated his arguments in my talk.
As every public speaker knows, a talk has to be practiced a number of times in front of a live audience before it gets good so I took it out on the road to schools and mathematical societies. The first of these was for the Isle of Man Mathematical Society. The night before I reread Brown’s paper to refresh my memory and understanding. But doubts began to appear. Perhaps due to my ignorance of music – I don’t play any instruments or sing – I had accepted his word on a number of assumptions but only then did I begin to examine their validity. Thinking of questions I might be asked I began to question various aspects of his argument. Less than 24 hours to the first performance and I was already in trouble.
The original recording
At this stage some background is probably needed to explain why I was having doubts. When I say that I’m interested in the opening of A Hard Day’s Night people look at me quizzically and say ‘Why don’t you look at the sheet music?’ or ‘Wouldn’t it be a good idea to ask one of the Beatles?’ The answer to the former question is simple: it doesn’t say. The latter is a more productive line of attack. Someone did ask George Harrison, the one who played the chord on his 12-string Rickenbacker guitar. His answer was ‘It is F with a G on top (on the 12-string), but you’ll have to ask Paul about the bass note to get the proper story’. (The standard reference for this is that Harrison gave this explanation in an online Yahoo chat on the 15th February 2001. I have been unable to find a Yahoo website containing the interview but a transcript is given here.)
If like me you are not musically inclined, then a translation may be needed. The standard Western musical scale has 12 notes in an octave. We have A, B, C, D, E, F and G (the white keys on a piano) plus some sharps and flats (the black keys). The A notes in different octaves sound similar but have different pitches, the B notes sound similar and so on. For a chord more than one note is played. A standard F chord consists of F, A and C. What Harrison means by ‘F with a G on top’ is that he plays the F, A, and C and then adds a G with a higher, rather than lower, frequency – hence the ‘on top’.
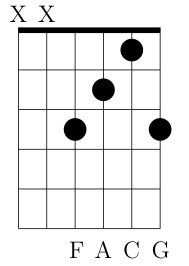
On a 6-string guitar this is easy to play. You only need to strum the 4 lower strings whilst holding the following pattern. (The Xs indicate strings that are not strummed and the dark bar denotes the end of the frets.)
The trouble is, it doesn’t sound like the recording. Even if you add a bass guitar and use a 12-string like Harrison’s, it still doesn’t sound right. It’s similar but it isn’t right. Something is missing.
The reason is simple. The opening chord isn’t played on a single guitar. More instruments are involved. The recording session details are known and we have a good idea of who was playing what that night:
- George Harrison, electric 12 string guitar,
- Paul McCartney, electric bass guitar,
- John Lennon, acoustic 6 string guitar,
- Ringo Starr, drums.
Now, even if you try playing all these instruments together with some supposed version of the chord, it still lacks authenticity. You can get close but it won’t be perfect. The answer lies in a hidden fact. It isn’t just the four Beatles playing. Someone else was in the studio with them. Someone whose contribution was crucial to the overall sound. The final person is their producer:
- George Martin, piano.
His piano playing adds the underlying thundering that powers the final chaaang. On the published recording the piano is evident when you listen for it but it is so expertly mixed into the sound that you don’t so much hear it as feel it. Our ears hear the shimmering ringing sound that comes from Harrison’s 12-string but the aggressive punch comes from the piano.
This means that to find the secret of the chord we will have to dig deeper than the explanation from Harrison.
Do my ears deceive me?
In addition to the why-don’t-you-ask-a-Beatle question I’m also asked ‘Why doesn’t a good musician just listen and tell you what it is?’ Another good idea. I am amazed by people that can listen to a piece of music and announce ‘That’s an F’ or ‘I’m detecting an A in there’. To me it is like magic, I can just about tell when one note is higher than another but as to where one is in the musical scale of A to G is beyond me.
There are however, many people who can perform this trick so maybe we should ask them. It turns out we can ask someone who managed to get some inside information.
Randy Bachman is a highly respected guitarist. Many people know his work, even if they don’t know his name. The 1974 track ‘You Ain’t Seen Nothin’ Yet’ with it’s catchy guitar riff was probably the biggest hit for his band Bachman Turner Overdrive. (Possibly you know it, see this video on YouTube for a reminder.) In recent years he has presented a radio show, Vinyl Tap, for CBC in Canada. In one show he performs the chord and relates the story of how he had the opportunity to hear the original master tapes of the recording. (The story is related in part 2 of Guitarology 101 starting at 30:24.) He was invited to Abbey Road Studios by George Martin’s son, Giles, to listen to Beatles recordings. Martin asked him what he would like to hear. There was really only one possible answer, the original tapes of the opening of A Hard Day’s Night.
The crucial point of his story is that the master tape is made up of multiple separate tracks that play simultaneously. In the early sixties tapes generally had four. The advantage of such a tape was that different instruments could be recorded on different tracks, possibly at different times, so that the volume of the individual tracks could be adjusted to get the final ‘mix’ just right. The piano on A Hard Days Night is a case in point, it was recorded by George Martin and added to the track later.
For our analysis what is good about having separate tracks is that each one can be listened to separately, you just turn down the volume on the others. So what did Bachman hear? In his broadcast he explains that Giles let him listen to these individual tracks: ‘So he put up one track at a time because when you hear it all at once it is like Bang! It’s the greatest thing to hear all at once. I heard the first chord. It was George on a 12-string just like this and it’s an F chord. [Strums 12-string guitar] But you put a G on top. [Strums] And you put a G on the bottom. [Strums]Then you put a C next to that G.’ In the subsequent explanation he has to be reminded by a fellow musician that McCartney plays a D on bass and claims that Lennon is playing ‘a D chord with a sus4, which means its got a G note on it.’
He then plays the chord on a 12-string accompanied by a bass and acoustic guitar playing the other Beatles’ parts. Though lacking the piano’s punch the resulting sound is very convincing – the audience’s wild cheer tell us that they, at least, are convinced. Listening to his version I was impressed at how close it sounded. True, if you play his version and the original side-by-side then one can detect differences but it still sounds very close. But is it really the chord? I’m going to stick my neck out and say that Bachmann is mistaken. I’ll explain why later. But how can he be mistaken? This is a professional musician, someone who works with music all day, surely he should get it right. To make matters worse, others have listened to the recording and claim all sorts of notes are audible. (See Pedler’s book for example.) Bachman is more believable because he heard the chord almost by itself without all the other instruments. However, ears are easy to fool.
Steve Jobs bragged when introducing the iPod that with it you could fit 1000 tunes in your pocket. At the time that was a lot but that number came at a price – the loss of quality. Listen to your favourite tune on an MP3 player such as an iPod and you can be forgiven for not realizing that a lot of it is missing. MP3 files rely on an interesting fact. Our brains fill in missing sounds. It is fairly well-known that we can fool ourselves visually by optical illusions – basically our brain attempts to fill in missing details and gets it wrong. Fooling our ears is an integral part of the theory behind the MP3 format. In it the song is compressed using some fancy mathematics. The original signal is broken up into pieces and for each piece the frequencies are analyzed. If one band of frequencies is particularly loud compared to the others, then some of the quieter bands of frequencies can be discarded as during playback they will be masked by the louder sound. Throwing away this information means that less space is required to store the song. The resulting sound is described as ‘too artificial’, ‘plastic’ or ‘hollow’ by critics but most people are oblivious to this reduction in quality and welcome the ability to store more on their player.
Now we need a little more theory to pick apart the chord. In principle a string plucked will vibrate backwards and forwards – the number of times it does this per second is called the frequency and is measured in Hertz (abbreviated to Hz). So 110Hz is a vibration of 110 times every second. In reality however, when we hear a plucked string we hear a collection of frequencies. The loudest frequency is called the fundamental frequency and – most of the time – will be the tone we perceive. In addition, the string produces frequencies called overtones or harmonics. The harmonic frequencies are whole number multiples of the fundamental frequency. For example, if the fundamental frequency is 110Hz (this is an A), then the harmonic frequencies 220Hz, 330Hz, 440Hz, 550Hz and so on are produced. The volume of each frequency will depend on the instrument and that’s why different instruments sound different – they produce different harmonics.
In the above I said that the loudest frequency will be what we perceive. An important part of the argument I am going to make later regarding the mystery chord relies on the observation that the loudest frequency is not necessarily the frequency corresponding to the note played. Having said that we’ll see that in the wrong hands, information gathered by mathematical means can also fool us!
We can work it out – The Fourier Transform
If our ears are untrustworthy and we can’t get the full story from the Beatles, how can we discover what they were playing? We unleash the power of mathematics. In particular the study of how heat propagates through an object. To understand this method we need to travel back in time…
Any sketch of the life of Jean Baptiste Joseph Fourier in an essay such as this will be incomplete. He had an eventful life. He was orphaned at the age of ten, escaped execution in the French Revolution, was a close advisor to Napoleon, governed Egypt for the French, publishing a seminal text on the country, and mentored Jean-François Champollion the man who deciphered hieroglyphs, has his name on the Eiffel Tower and is credited with discovering the greenhouse effect. And it is not even any of these that are relevant to the Beatles story.
Joseph Fourier was born on the 21st March 1768 in Auxerre, France. In his early life he wavered between a career in mathematics and one in the priesthood. He was certainly a talented mathematician having consumed Bézout’s Cours de mathématiques by the age of 14. Not that he was happy with his talents, he wrote ‘Yesterday was my 21st birthday, at that age Newton and Pascal had already acquired many claims to immortality.’
Instead, in his early twenties, he became an organizer in a local revolutionary committee and as the French Revolution played out he was imprisoned and naturally faced the possibility of execution by guillotine. The revolution was a chaotic time with different groups attaining power at different times, people rising and falling from favour and Fourier was subsequently released as power shifted.
Unhappy and perhaps wary of the dangers of politics he returned to mathematics. By 1795 he was teaching in the École Polytechnique and only 2 years later succeeded Lagrange, one of the greats of French mathematics, through an appointment to a chair of analysis and mechanics.
His life took another turn when in 1798 he was one of Napoleon’s chief scientists in the French invasion of Egypt, a post that led him to write a seminal book on the country. His life ended following a fall down his stairs at the age of 62. According to reports he thought that the secret to good health was to wear lots of blankets when at home. In his case this led to a tragic accident.
His continuing fame within science arises from the book, Théorie analytique de la chaleur, (The Analytic Theory of Heat), published in 1822 though mostly presented much earlier in 1807.
Until his book no one could give a convincing mathematical description of how heat propagates through objects. His resulting methods have found application throughout the modern world. In our case, rather strangely perhaps, the key to analyzing sounds has it roots in the theory of heat. Here we have a perfect example of a theory that has unexpected applications in other areas.
The book was not without controversy. Fourier’s central method was to decompose waveforms into sines and cosines. That is, you can build any function by taking an infinite sum of sines and cosines. In fact, this was a concept already explored, for vibrating strings, by Daniel Bernoulli about fifty years before Fourier (so perhaps Fourier series should be called Bernoulli series).
A sine wave and cosine wave look the same so we shall just talk of sine waves. The picture below depicts a sine wave.
If you hear this it will be a single frequency rather than a collection. The height represents loudness and the spacing between the peaks gives the frequency. A sine wave with peaks closer together will produce a higher frequency.
For a general piece of music, the resulting waveform will be very different to a sine wave, in close up it will have a lot of jagged ups and downs.
A central claim of Fourier was that any waveform can be written as an infinite sum of sines and cosines. The great mathematicians of the time, such as Lagrange who had his own competing theory of heat, had a hard time accepting Fourier’s claim. In essence, their argument was that sines and cosines are very well behaved waveforms. For example, you can apply a well-know operation to them called differentiation as many times as you like. Any sum of these nice waveforms should then be nice, for example differentiable as often as you like, and hence there is no way you can make a non-nice waveform from nice waveforms.
The escape from this reasoning is that Fourier’s claim is that you use an infinite sum of sines and cosines. The world of the infinite is home to many strange ideas and one soon encounters counter-intuitive results.
We can see this quite readily and see the flaw in the critics’ reasoning by considering what happens when we add together an infinite collection of positive numbers. Intuitively, it feels that adding an infinite collection of positive numbers that the answer must be infinite. After all, adding them one by one means that the total gets bigger and bigger.
Now, let’s consider an example and add 1/2, 1/4, 1/8, 1/16, 1/32, 1/64,… (where the dots mean we go on forever). Each term of the sequence is half the one before. The total for this is not infinite but is equal to 1. To see this we start with a circle.
Shade half of the circle. This correspond to 1/2 in the sum Now shade half of the unshaded part. That is shade in 1/4 of the circle. Next, again shade in half of the unshaded half. This is 1/8 of the circle. Repeatedly applying this process of shading half of the unshaded part is the same as adding 1/2, 1/4, 1/8, 1/8, 1/16, 1/32, and so on. Note that by definition, the shaded part (equivalent to the total of the sum so far) can never go outside the circle and so the final sum cannot be greater than 1. By repeating the process again and again we can shade any given part of the circle so the sum cannot be less than 1. Therefore as the sum cannot be less than 1 or greater than 1, the sum must be 1.
This shows that the idea of infinity leads to unusual, non-intuitive results and a German mathematician called Dirichlet proved Fourier (and Bernoulli) right. Well almost. The world of functions is sufficiently wild to allow functions that cannot be written in the way Fourier stated but these can be safely ignored in this essay. (In fact Fourier was well aware of the difficulties. Explaining these precisely is hard in an undergraduate course never mind an essay such as this.)
In summary, infinite sums of sines and cosines greatly simplified the theory of heat transfer. Fourier’s main contribution to the theory was he gave formulas for working out the amplitudes and frequencies. A quick way of doing this is to use what we know call the Fourier transform which is written mathematically as:
If you are unfamiliar with the mathematical symbols, then don’t worry. I include this formula only to point out that this theory involves
In summary, Fourier’s method takes a waveform and blows it apart into its constituent frequencies and tells us how loud those frequencies are. The loudness is called the amplitude. Therefore, if we have a piece of music we can apply the Fourier transform to it and, in principle, discover the notes that make it up. And that’s precisely what we want to do to the Beatles’ magical mystery chord. All we need is software to calculate the Fourier transform, hence the frequencies and amplitudes, and from these determine the notes played in the chord. This is the method employed by Jason Brown in his analysis of the chord. In 2004 Brown received considerable media attention for his claim that he had applied the Fourier transform to the chord and had isolated the notes. This appeared to settle the question and was widely believed.
Brown’s Analysis
Let’s now see some of the details of his argument. First he applied the Fourier transform to ‘approximately one second in the middle of the chord’ (The quote and analysis given here can be found in Brown’s paper.) He found 29,375 frequencies observing that this includes the frequencies of the notes played and their harmonics (and possibly other artefacts caused by rattles, etc). This is too many to handle so he whittles down the collection. Brown outlines his method: We are after the loudest notes, as these correspond to the fundamental notes being struck… A threshold was chosen which kept the sound faithful to the original. The table shows the 48 frequencies with amplitude 0.02 or larger.’ He then gives the table which I reproduce here just to show how messy the output is despite being cut from 29,375 frequencies down to just 48. Don’t worry, you don’t have to understand the table – it is included just to show how messy this analysis is.
The table is hard to comprehend but Brown’s process is simple: find all the frequencies and select the loudest ones as they will be the notes played (and possibly their harmonics). His further analysis determines who plays what. I’ll outline the ideas rather than all the details.
Note that the first nine frequencies are (the grouping will make sense later)
110.34,
145.619,
148.621,
149.372,
150.123,
174.142,
174.893,
175.643,
195.159.
Note first that the second to fifth frequencies found are all close to one another. They are in the range 145.619Hz to 150.123Hz. What is going on here is that four notes are played but since instruments are never tuned to exactly the right frequency they are all slightly different. The note nearest to this collection of frequencies is a D which is 146.832Hz. The amplitudes provide further clues. The frequency 150.123 has by far and away the biggest amplitude out of all 48 notes and so is probably a single note played on a single instrument – a particularly powerful instrument as the amplitude is still large in the middle of the sample of the chord. A good candidate for this is a D on the bass guitar which is exactly the note that Randy Bachman had trouble remembering. It is traditional for bass players to play single notes at a time so it most likely McCartney.
That’s one frequency identified – we’ll not do the remaining 47. Brown’s analysis of who plays the other three Ds is detailed and introduced the idea that when a piano note is played we don’t just hear one string vibrating we in fact hear two or three as most pianos have more than one string for each note. The hammer hits not one string but two or three all tuned the same. This is key to Brown’s solution and he relates how he went to a music shop to check it. In fact, this is quite a good idea, it is unfortunate that it gives the wrong answer. (I suspect that this is because the software used can’t accurately distinguish two closely tuned strings.) The idea allows Brown to attribute multiple frequencies to George Martin playing the piano.
He reasons that George Harrison is playing one of the Ds because of the nature of a 12-string guitar. A 12-string guitar is tuned so that strings are paired up.
The top string is tuned to E say and the next one in the pair is also tuned to an E but one octave higher. To distinguish between notes in different octaves we shall use standard scientific notation for octaves. The lower E on the 12-string is called E2 and the higher one E3 – these correspond to frequencies 82.407Hz and 164.814Hz respectively. (Note that the frequency of the second is double that of the first.) The next higher E would be called E4 and so on. Rather confusingly an octave starts at C and so the run of notes is, for example, F2, G2, A2, B2, C3, D3, E3, etc.
A standard 6-string guitar is tuned E2, A2, D3, G3, B3, and E4 from lowest to highest frequency. A 12-string follows this and is tuned as E2 E3, A2 A3, D3 D4, G3 G4, B3 B3, E4 E4. That is, the strings are tuned in pairs with the first four pairs having the pair of strings tuned an octave apart whilst the last two pairs are just in effect doubled up, i.e., each string in the pair plays the same frequency.
This system of paired tuning implies that if Harrison plays a D in the chord then he is playing two Ds, a D3 and D4. The frequency of a D3 is 146.832Hz. Since a change in octave just involves doubling the frequency we should expect a frequency of about twice 146.832, i.e., 293.664Hz to appear as well. Looking at the table we see that there is only one such frequency, at 299.494. This fits with Harrison playing a D since he has no option but to play the other at the same time.
With similar reasoning Brown excludes Harrison from playing an F. If Harrison played an F3 which is about 174Hz, then he would have had to play an F4 at about 348Hz and there is no note near that in the table. Therefore, Harrison does not play an F. Note that this flatly contradicts what Harrison and others, including Bachmann, says he was playing.
Anyhow, the preceding gives a flavour of the reasoning employed by Brown. His final solution for the chord is
- Harrison: A2 A3, D3 D4, G3 G4, C4 C4
- McCartney: D3
- Lennon: C5
- Martin: D3 F3 D5 G5 E6
That would seem to settle the problem. From my initial perspective, for my British Science Festival talk this was a good result. It used mathematics to produce an answer that no one had suggested so far. Not only that he had used the hidden fact that piano notes are made up of more than one string vibrating. Hence, preparing my Auto-Tune talk I was eager to include his results.
As I said, reviewing my talk the day before first presenting it, my doubts emerged. For example, why is Lennon, the song’s composer, only playing a single C on his guitar. It is odd to play one string rather than a chord if one wants to satisfy George Martin’s demand – a dramatic opening. Furthermore, it is quite a high C – more of a ping than a bang. A very peculiar note to play in the context.
What of Brown’s claim ‘We are after the loudest notes, as these correspond to the fundamental notes being struck’? Is that always true? Do loudest notes correspond to notes played? Also, why is the cut-off 0.02? If Harrison had played an F3, then the higher F, the F4, may, quite naturally, have had lower volume or decayed so quickly that by the time it was sampled its amplitude was just below 0.02 and hence would be absent in Brown’s table despite being played.
The first few times I gave my talk on Auto-Tune I was unhappy with it, mainly because of the chord analysis rather than anything else. Was I merely presenting a good story rather than presenting sound mathematics? In such situations, a true mathematician has only one option: I would have to solve the mystery of the chord myself.
Researching the chord
In years past academics would research for years in dusty libraries, looking for facts hidden amongst thousands of books. These days we have the internet and search engines that give immediate answers. It makes for less romantic stories of discovery. It is more efficient and for me particularly useful as the British Science Festival was only a few months away.
After an initial trawl of the internet I found that I needed Dominic Pedler’s 40 page article on the chord. His book Songwriting Secrets of the Beatles was in the basement of the impressive Brotherton Library at my university and gave me the chance to indulge my passion for an old-school search and rummage in a dusty library.
After taking a book from the shelf I skimmed a few pages. What jumped out at me on this occasion destroyed any belief I had left in Brown’s analysis. My flicking had stopped on a page with the section title ‘The right channel – the crashing piano’. The implication of those words was immense. There is a stereo version of the song! Most early to mid 60s records were released in mono, i.e., you need only one loudspeaker. Only later was stereo standard. Ie., different sounds coming out of two different speakers, referred to as the right and left channels, one for each ear. I had assumed that A Hard Day’s Night was in mono – certainly, Brown had never mentioned separate channels. In this case since the track was to be on a film soundtrack it was also released in stereo.
The reason for my excitement at the discovery of a stereo version lies in my teenage interest in rock and roll. I collected recordings by Rock and Roll artists such as Eddie Cochran, Little Richard, and Chuck Berry (all influences of the Beatles) and knew that many early 60s stereo records do not have the instruments evenly distributed between the channels. Instead producers often put some instruments wholly on one channel and some wholly on the other. This made rare stereo versions great fun as one could, for example, restrict the sound to hear just Eddie Cochran and his guitar on one channel or restrict to the other side and hear only the rhythm section. (You can hear this on Portrait of a Legend, in particular Cherished Memories and Jeannie, Jeannie, Jeannie.)
Therefore, a stereo version of the song was potentially the greatest asset in analyzing the chord. And indeed, the stereo version is mixed so that, more or less, Harrison and McCartney come out of the left speaker and Lennon and Martin come out of the right. This eases the analysis. Just feed one channel into the Fourier transform, discover what Harrison and McCartney are playing and then do the same for Lennon and Martin channel. In this way we avoid disentangling Harrison and Martin say as Brown had to. A serious analysis has to study the left and right channels separately.
Checking the book out of the library and taking it home I found that Pedler’s article has much more than the stereo revelation. It introduces and discusses all the main events during the recording of the song. The Beatles had numerous attempts at recording the song — each attempt is called a take — finally requiring nine for this song, some of which lasted only a few seconds due to one of the participants messing up. As these recordings were made available in an unauthorized bootleg the development of the song and in particular its opening can be traced. For example, it can be heard that Lennon swapped his electric guitar for an acoustic between takes 3 and 4. (A detailed collection of the takes can be found here.)
At this point it is worth mentioning Pedler’s preferred answer to the mystery. He believes that Harrison and Lennon are playing the same chord on their guitars: an F with a G on top, which is usually called F with an augmented ninth and denoted in music by Fadd9. (This is as Harrison describes.) McCartney plays a high D, i.e., a D3, and their producer, George Martin, plays D2, G2, D3 on the piano. This conclusion came from hours of repeatedly listening, some Fourier series software and of course as we must all do, some guesswork.
Prepared with the lessons from Pedler I was ready to attack the chord and discover its secrets. It was clear that solving the mystery required Fourier analysis software. One can use a mathematics package such as Matlab as Brown had done. But that led to too many frequencies and even when narrowed down, the answer is still unclear because, even for a mathematician, a table of numbers is hard to analyze. A more visual method was preferable. The ultimate software would produce the notes in a standard music notation for each instrument but no such software exists.
Good software does exist though. In my investigation of Auto-Tune I had discovered Melodyne. This allows analysis and editing of music. In theory you can record a chord, feed it into Melodyne and then alter the individual notes in the chord — one may wish to retune an out-of-tune guitar string. In other words it allows you to blow apart some sound, change it and use the new version. Never before have musicians had such astounding musical editing machinery.
I purchased a copy of the stereo version of A Hard Day’s Night and fed it through my recently downloaded free copy of Melodyne. (The track was from a CD and therefore suffers from compression issues. That is, some of the frequencies may be missing due to the method employed to fit everything on the CD.) Like most software it takes work to familiarize yourself with it but despite this I quickly got some interesting results from the song without separating the channels.
In the following screenshot we can see a list of notes down the left side. The lines and splodges represent the volume of the notes as the time progresses. The opening chord is made up of a number of almost continuous lines and to the right of those the blobs represent the notes as the song is played.
My attention was caught by the D, represented by a small blob in the bottom left. Everyone agrees that McCartney was playing a D, so it was pleasing to me that there is clearly D at the bottom of the screen shot. Pleasing until I realized that everyone agrees it is a D3 and the Melodyne was telling me it was a D2. Intriguingly, everyone agrees that in later performances of the song such as on Live At The BBC he played a D2. Fortunately, Pedler mentions that earlier Fourier analysis had noticed this and he suggests that McCartney perhaps softly struck the lower D in addition to the higher D.
The output from the left hand channel (with McCartney and Harrison) was clearer. The D2 is more prominent and lasts longer in this output.
Looking carefully, one can discern a quiet F2 not the usual F3 suggested by Pedler, Brown and others. This deepened the mystery but given that Melodyne is like any piece of equipment, it takes time to learn it and interpret its output, there was always the chance for error. It sometimes gives harmonics as notes played. For example, no one claims that a B was played but there was clearly one in the picture I got for the right channel (with the piano). What is likely happening here is that the software is picking up an exceptionally strong harmonic and assumes that it is a played note.
Analysis of the left and right channels separately provided the following. The left with McCartney on bass and Harrison on the 12-string was very clear but there was a lot going on in the acoustic 6-string and piano (Lennon and Martin) channel. There were clear Fs in the Harrison channel, contradicting Brown’s analysis of the chord and backing up Pedler. To be fair, the pictures did not conclusively prove that the Brown is wrong, after all the software uses a complicated algorithm which even its inventor claims can make mistakes.
Ultimately, the Melodyne output was not as conclusive as I had hoped though intriguing new clues were found. More was happening in the lower frequencies than Brown’s study had revealed. He said that below 110Hz (an A2) there was nothing of interest. The Melodyne algorithm contradicted this. There was a lot going on. But it wasn’t clear what. Did McCartney really play two Ds, one a low D played softly and the other a higher D, the one everyone hears or did he just play one? If he did just play the high D, as everyone says, then what is going on at the low D frequency? Did someone else play it? It was too low for Harrison’s guitar.
The crucial tool for further analysis came, like many discoveries do, from a chance conversation. My colleague Margit Messmer uses a program Transcribe for practicing the saxophone. As the name suggests it can used for transcribing music. It analyses a piece of music and, rather than a table of numbers or blobs on a screen, shows the Fourier transform output in a very visual, easy-to-understand form by matching the frequencies to a piano keyboard. A spike indicates that a frequency is present, either as a fundamental or as a harmonic, and the height represents the volume of the frequency.
The following picture shows the Transcribe output from a D2 played on a bass guitar.
The leftmost spike is the frequency of the note and the other spikes are the harmonics. Imagine what the table of numbers would look like. This is very clear as one can see where the frequencies fall on a piano.
Now, let’s see the output from the mono version of A Hard Day’s Night.
Look down at the low end. A D2 and F2 clearly appear if only softly, confirming the presence detected by Melodyne. (And contradicting Brown and Pedler’s analyses). Recall that the heights of the peaks represent the volume of the frequency. The higher the peak the louder the frequency. Observe that heights of the peaks in the puzzling low frequency range are lower than the other frequency ranges. This is the key to the following argument and the solution I am about to propose.
We start with a ‘what-if’ argument? What if McCartney really did play a D2, i.e., the low D, and did not play the D3. In this case we would see a spike at the D2 frequency, i.e., 73Hz and we would see spikes at all its harmonics, i.e., 146Hz, 219Hz, 292Hz, and so on. The first of these, 146Hz, is the frequency of a D3. In other words, if McCartney plays a D2, then the frequency of a D3 will automatically appear.
Now if McCartney plays a D3, the high D, then the frequencies arising will be 146Hz, 292Hz, 438Hz and so on.
Comparing these two lists we see that a D2 will produce the frequency 219Hz (this is an A) and a D3 will not. A useful Transcribe feature allows us to place the mouse pointer over a frequency and vertical lines appear where the corresponding harmonics are. In the following picture of the left channel we can see that all the harmonics for a D2 are present.
There is something happening at 219Hz (the A to the left of mid C). Leaving aside the possibility that someone is playing an A this is good evidence for a D2 being played.
The problem is then, why is the D3 harmonic louder than the D2 that caused it? Harmonics tend to be lower in volume than the fundamental note. How to solve this puzzle? Well, music producers alter the volumes of individual instruments to produce a nice mix. They also alter the volume of frequency ranges. A bass guitar is a powerful instrument and if you don’t turn down its lower end frequencies then the sound can be indistinct, it sounds ‘muddy’. If someone recorded a D2 and turned down the frequencies around D2 but not the higher ones then the loudest frequency would in fact be a harmonic, such as a D3. Furthermore, the note heard might sound like a D3 and not the true one, the D2!
This is seen in the next diagram which is the D2 we saw earlier but with the bass notes turned down. The inserted box shows how the volumes are reduced in the bass range.
Thus we get another case where our ears deceive us. A D2 is played but due to the producer altering the sound, we hear the wrong note! We hear a harmonic, the D3. So my guess is that McCartney was playing a D2 just like he does in the live recordings – presumably the mixing engineer for the live recordings did not mess around with the bass frequencies and cause us to hear the wrong note.
The crucial claim for the subsequent analysis of the chord is that the bass frequencies have been turned down.
Let’s now see what implications this has for Harrison’s 12-string guitar which is on the same channel. The frequencies are not quite consistent with the Fadd9 that Harrison and Pedler claimed as there are some extra ones. In fact rather than FACG, it looks like we get an extra lower F and A and these have been turned down as they are in the bass range.
Let us suppose that Harrison played this FAFACG rather than the FACG. It is possible to play this new shape on the guitar by holding the one for FACG and then hooking the thumb over to hold the top string at the second fret. This gives the F and leaving the other string unfretted we get the A. Interestingly, in video of the Beatles playing the song live this is precisely the hand shapes that Lennon and Harrison hold. This is pleasing and somewhat tantalizing but of course is not conclusive evidence that this is what they played on the record.
This solution – a low D with a FAFACG – is very satisfying as it fits with the evidence from Harrison – it is still an F with G on top. (My colleague Rob Sturman has suggested an interesting point: with the bass D note one could call the resulting chord D7sus4 which is similar to what Bachmann said Lennon was playing when he heard the original master tapes at Abbey Road.)
We can now turn to the right hand channel with Lennon on acoustic guitar and Martin on piano.
The messy right channel
This solves the mystery of what McCartney and Harrison are playing but what about Lennon and Martin? This was much harder to do. The right channel is pictured below.
Comparing to the left hand channel one can see there is plenty more going on in the right hand part of the output. We are probably seeing a lot more harmonics. This is probably telling us that more notes are played by Lennon and Martin than by McCartney and Harrison.
From reading Pedler it seemed likely that the piano was played with the sustain pedal down. This makes analysis really, really difficult because all the strings are free to vibrate. When the chord is struck any string that is tuned to a harmonic will move in sympathy with that harmonic. This could explain the presence of the B that people often hear in the chord. It may just be the sympathetic vibration of a B string in the piano. For example, B4 is the fifth harmonic of G2. The upshot of all this is that the right channel is a lot messier in terms of harmonics.
Looking at the output there is clearly an F and an A occurring in the same place as the extra F and A played by Harrison. At this stage it is reasonable to assume that on his 6-string acoustic Lennon was playing the same chord as Harrison. This is a not a big assumption but is an assumption all the same and furthermore it doesn’t help with the analysis of the piano.
By carefully analyzing the harmonics like in the bass case I produced an answer for the piano notes. Given that I have no musical training or ability, this, in all honesty, was nothing more than an educated guess based on what Pedler had written and on my limited understanding of musical theory.
As a solution to the A Hard Day’s Night problem it wasn’t very convincing. It certainly wasn’t convincing me. I had visions of my British Science Festival talk being a major humiliation with people asking awkward questions I couldn’t answer and criticizing the high level of guesswork. After all, I was only confident of Paul and George’s contribution and had fudged the answer for Lennon and Martin. That’s not a satisfying talk. It’s only half the story and not a solution to the mystery. I couldn’t even be sure that Lennon was playing the same as Harrison, that was just a reasonable guess. Sure, I could give the talk but if I’m not convinced with half an answer who else will be?
Deliverance from embarrassment came from idly surfing the web. I found a website ridiculing Brown’s analysis. Not only that, Transcribe had been used to show what Lennon and Martin were playing on the tricky right channel. Any researcher will tell you how deflating it is to find someone had already produced your clever answer or solution and had effectively beaten you to the punch by publishing first. It has happened to me before with my own mathematical research. (It is usually accompanied with a horrible sick feeling in the stomach.) In this case, I was working in a subject I was unfamiliar with and so in many ways I was happy that someone had come up with an answer that was similar.
What was really annoying though was that he had a far, far better answer.
The website’s author, the humorously named Waynus of Uranus, had convincing evidence that Lennon was playing the same as Harrison. The evidence is clever and elegant. Not only that the underlying method is a bit of mathematical trickery that would look great in a talk. I was back in the game for a triumphant talk at the science festival even if it wasn’t my work. And all I had to do was verify the author’s method.
All you need is ‘Love’
Recall that that George Martin’s son, Giles, invited Randy Bachman into the Abbey Road Studios to listen to the original master tapes. What was Giles doing there? Well, he was remixing Beatles tracks for a show by the modern circus, Cirque du Soleil. The results were issued on an album called .
It turns out a remixed version of the chord appears between the first and second songs on the CD. In other words we have a stereo version of the chord which will have the same notes but the frequencies will possibly be mixed differently. What would analysis of that produce? More than I expected.
The new analysis is not Fourier analysis but a technical process called phase inversion. The effect is rather magical. Given a stereo track phase inversion can knock out the vocals leaving only the instruments and so the vocal-less track can be used for karaoke performance.
In general, once a song is recorded and mixed into two channels for stereo, there is no way of undoing the process, Melodyne not withstanding. Nonetheless, certain parts of the track can be eliminated. In contrast to early recordings producers do not put instruments wholly on different channels. They now spread the instruments across the stereo speakers. Usually the vocal track is balanced evenly between the two channels so that it appears to come from directly between the speakers whilst other instruments might come from slightly to right or left. For example piano to the right and rhythm guitar to the left.
To see how phase inversion is going to help us suppose that we have recorded a song without vocals on it. This means we have two waveforms, one from the left and one from the right and these waveforms are different because effects have been added to move the instruments to slightly the left or right. Call these waveforms L and R for left and right channels respectively.
When we record the vocals we produce another waveform, call it V. Now we add the vocals to our track. Since we want it to sound as though it is exactly in the middle of the speakers we add this waveform to the left and right channels in equal volume. Putting it onto one side with more volume would cause the vocal to sound closer to the corresponding speaker. Once the vocals are added to the song it would seem that there is no way we can remove them but we shall now do so.
Our situation is that we have two waveforms, R+V and L+V, each containing the vocal track in equal measure. We ‘invert’ one waveform, L+V say, by turning it upside down, to get -L-V. We add this to the R+V waveform. What is the result?
The resulting waveform is R+V+(-L-V)=R-L. In other words, we produce a new waveform containing no vocal element. It is merely a waveform made of the instruments. The vocal tracks in the left and right channels have cancelled.
In practice, the effect is not perfect, if you listen carefully then you can sometimes hear the vocal and you can lose other instruments that were mixed into the middle, for example the bass drum is commonly mixed to there. The important point in our case is that with a phase inversion we might eliminate an instrument or two and thus make the other ones clearer.
Waynus of Uranus fed the Love remix of the chord into Transcribe and applied a phase inversion to it. The result is startling. Playing the phase inverted version one clearly hears an acoustic guitar — all the other instruments in the remix are effectively eliminated. The Transcribe output is just as clear. We see a waveform consistent with the FAFACG chord that the left channel analysis had given for Harrison’s 12-string. But better still, Transcribe makes a guess as to the chord. Guess what? It says Fadd9. Exactly what we want. Exactly what Harrison said.
The solution now takes shape. So where do we stand? We have McCartney, Harrison from Fourier analysis and Lennon from phase inversion. Note that we have two distinct methods giving the same answer so our confidence grows immensely. All that remains is Martin’s piano part. This is the most challenging.
In the end, for my talk I decided to use Waynus’ answer rather than my own. Waynus appears to be a musician and so any answer will carry more authority than mine. (And for me the mathematical points have been made.) The final answer arises from careful analysis of harmonics. This is complicated — remember that the bass frequencies are assumed to be turned down — and so the details will be omitted but can be found at Waynus of Uranus’ site.
Waynus’ final version for Martin’s piano part is D2 G2 D3 G3 C4. (My version did not include C4. Note that Pedler’s version does not include the G3 or C4.)
In the studio
With just a few weeks to the British Science Festival I had an answer. Ok, it wasn’t wholly my answer but I had done enough to convince myself that the notes were, if not exact, near enough. The ultimate test is to reproduce the chord and let other people decide. Randy Bachmann had impressed his audience with the authenticity of his version but, to my knowledge, Jason Brown had not recorded his version for us to hear.
My inner showman wanted the chord to be performed live at the Festival but due to the difficulties in securing the instruments — 12 strings and grand pianos are hard to come by — I abandoned that idea as impractical. Great as a live performance would be I settled for a pre-recording. Now the only problems to overcome were that I cannot play any instruments and certainly don’t own any.
I was not going to be giving the BSF talk alone. My colleague at the University of Leeds, Rob Sturman, would also be presenting. His talk is about how the accepted tuning system we use in Western music is in fact not in tune. All the notes are ever so slightly out. This surprised me and perhaps surprises you. It was Rob that solved my problem of instruments. His brother-in-law, James O’Doherty is a professional musician and agreed to help.
Hence, one cool Friday afternoon in August Rob and I walked from the university to James’ house. James had been unable to find a twelve-string but had acoustic and electric six string guitars, a bass, and a keyboard which we could use for the piano part. In true do-it-yourself rock and roll style we recorded all the various parts in his bedroom.
For good measure we recorded the Brown version for comparison. His solution has Lennon playing a single C on his acoustic and my keenness to be on some sort of musical recording coupled with a lack of musical ability meant that this was my chance. All I had to do was fret one string and strike it. No knuckle-busting chord shapes required.
The recordings were made and I took home the ‘master tapes’, which these days are just digital files, to mix down to a final version. I experimented with various volumes for the different instruments but although almost immediately produced a chang that brought a triumphant smile to my face, none sounded authentic enough. The underlying problem was that we had used a keyboard in place of a piano. Time to go back to the studio for a rerecording.
Investigations uncovered various colleagues and friends with pianos. Unsurprisingly, all were willing to help but equally unsurprisingly none had a grand piano at home. Again, Rob came to the rescue and obtained access to a music practice room. As the nature of the legitimacy of our access was in a grey area I can’t tell you exactly where we recorded it. In fact the ‘sneaking in’ nature of the recording added to the fun. Once inside the studio I quickly set up the recording gear – my video camera with an external microphone attached – and recorded the piano chords.
Although the final recording is slightly distorted due to the amateur nature of the equipment it was enough. When mixed in with the other instruments the overall sound was, to my poorly educated ears, close enough to the original. After the final mix my brother, an accomplished musician, pointed out (as have others subsequently) that the bass is not loud enough but by then time was running out and I had to make a video to accompany the talk.
I quickly cut together video that I had shot during a trip to Liverpool with output from Transcribe. (The adventure of dashing around Liverpool with a taxi driver who was unsure of which Beatle had been murdered is a story in itself.) The voiceover was terrible as I was recovering from a cold. Nonetheless I had a chord and now a video uploaded to YouTube. Next stop the British Science Festival.
The British Science Festival
The festival organizers prefer talks to be given by two or three people – a single speaker lecturing for an hour or more is considered tedious. I had already teamed up with Rob Sturman and we completed the required trio with Ben Sparks. Ben is a school teacher I had met at a conference about public communication of mathematics. At the conference every table had to do something to entertain the other conference participants and so our table, for reasons that are not clear to me now (and perhaps not even then), rewrote the words to Video Killed the Radio Star as Video Killed the Algebra Star with Ben playing the musical accompaniment on guitar. From my perspective we would make a good team for the BSF talk — and I would be able to hide behind the other two should any musical questions arise.
The final talk was based around Rob’s talk on how western tuning is not in tune despite what one might think and my talk Auto-Tune talk with the Beatles’ chord now added. Ben would add explanations and demonstrations along the way. To give you some insight into our planning method we never met all in the same room until the day before the talk. Furthermore, we decided to have a practice before the talk but were given the opportunity to talk to the press about the chord and so actually spent most of our practice time talking to a journalist. Given that Rob and I had given our talks separately for many months and Ben had considerable busking experience so wouldn’t be fazed by extemporaneous performance, this wasn’t such a bad a state of affairs as it might appear.
The final set up was that Rob and Ben would do the first half and Ben and I would do the second. I am highly seasoned in giving talks and so nerves are not as bad as they used to be. In the past I used to travel to schools and other events with the classic knotted stomach promising myself I’ll never do this again, it is too stressful. These days I have given so many talks and had so many mishaps happen that little throws me anymore. However, this time the stakes were higher, my parents and my four-year old daughter were there. Fortunately, despite a major problem with the computer at the start of my section, everything went well. My volunteer from the audience did a great job of singing Loch Lomond for us and the audience laughed in all the right places. Afterwards my father said he was impressed – according to him I looked like someone who knew what they were talking about. High praise.
A good talk always leads to a high. What happened next added an extra layer. The journalist filed a report. By the time I got back to my parents house the story was already travelling around the world. Hundreds of news outlets picked it up and over the next few days I ended up being interviewed on various radio shows including, rather fittingly, Radio Merseyside.
Ok, but what does it sound like? Listen and compare with the original:
I know, I know, not enough bass…
There Will Be An Answer?
Where does this leave us? Is this the final word on the mysterious chord? Probably not.
In any analysis assumptions are made, for example Brown assumed that the fundamental frequencies are the loudest. Waynus of Uranus and I both assumed that the bass frequencies have been turned down.
Other assumptions have been made. I tried to apply Occam’s razor in my analysis by taking the simplest explanation. Yes, it is possible that McCartney gently played a low D and a louder higher D at the same time and in later performances he played a low D. But isn’t it more likely that he played the same note each time and some straightforward, commonly used recording techniques led to the D being perceived to be a high D? What if Harrison played a standard Fadd9 and Lennon played the version with the extra F and A and the F and A we hear on the Harrison speaker is in fact just sound ‘leaking’ through from the Lennon speaker. These and other possibilities cannot be wholly discounted.
I certainly have some nagging questions about points I can’t quite explain. For example, why does the chord differ from the one that Randy Bachman heard when he listed to the individual tracks at Abbey Road?
People will always have alternative theories. For example, the piano was recorded at a different speed or its strings were struck by opening the lid and strumming them rather than hitting the keys. These are all minor points I feel. To recreate the sound perfectly will always be impossible. Even if the Beatles had tried again something about it would have been slightly different. The question for me is how convincing is the sound? Would a casual observer tell the difference between them when played one after the other?
Shortly after giving the talk I received an email from someone with an interesting theory. They suggest that Martin had recorded the chord and then on top of that had recorded a new version with everything played at half speed. Messing about with speeds had already been done on the track with the recording of the guitar solo and piano in the middle of the song and so this is not far fetched. One simple consequence of adding a half speed version over the top of the chord is that it would produce the extra F and A in what Harrison plays from a simple four-string FACG.
Maybe one day, George Martin will tell us what he did. Maybe someone will, like Randy Bachman, get access to the individual tracks on the original 4 track master and apply the Fourier transform. (If anyone with the security clearance to work with the Beatles master tapes is reading this, then I can be on the train to Abbey Road with my laptop at very short notice!) Probably, we will never know the answer.
Even if we did know the answer what would we do with it? Would we be able to create a new version that would fool the experts? And even if we did produce that, what is the point? If you recreate the Sistine chapel or slavishly copy the Mona Lisa, what is the point? For a musician copying someone else is an important part of learning. Certainly the Beatles learned a lot from copying Chuck Berry and Little Richard as is clear from their first album. But copying a single chord, is that worthwhile for a musician?
So what is the upshot of all this? There was a problem and it could be attacked with mathematics. An online commenter claimed he would be very angry if we had been given a massive grant to study the chord. This shows that there is a lot to be done to explain mathematics research to people. No one would ever get money for studying a Beatles chord. At least, I would hope not.
At the end of this adventure, I hope that you see that this was all done for pleasure — simply for the fun of it. I attacked a problem because it was interesting and I had a good time recording music and performing with Rob and Ben. I was disappointed at being beaten to the answer by someone else but my original motivation was achieved, my parents were able to see me give a talk. In the end all a bit of fun, not life and death. As Lennon wrote in Strawberry Fields, nothing to get hung about…
The Full Video
Appendix: How to play the chord
To play Waynus of Uranus’ version of the chord you will need:
- An electric 12-string guitar.
- An acoustic 6-string guitar.
- An electric bass guitar
- A piano.
For extra Beatles authenticity you can add a bit of Ringo with snare and bass drums.
- The guitars play the same F chord: F A F A C G.
- The bass plays a D2.
- The piano plays D2 G2 D3 G3 C4.
If you want to play it by yourself on a 6-string, then a commonly favoured method is to play G7sus4.
Acknowledgements
My thanks to my colleagues Rob Sturman and Margit Messmer who read an earlier draft of this essay, pointed out mistakes and made helpful suggestions.
Get the newsletter! Fancy a newsletter keeping you up-to-date with maths news, articles, videos and events you might otherwise miss? Then sign up below. (No spam and I will never share your details with anyone else.)




















Very cool analysis of the Beatles chord! With reference to Paul’s D2 with a strong D3, I have some input for you. I work on old tube amps and guitar electronics as a hobby, and I can tell you that because of the way the strings resonate hitting a D2 on a guitar will give you a lot of D3 overtone, in fact generally you get almost as much of the first octave up as the root note. Now, older amps such as they had in the 60’s could not accurately reproduce the lower frequencies – so the fundamental could have been effectively “mixed down” right in the amp, leaving mostly D3. You would still hear it as a D2 but with a sort of brassy quality to the sound.
Thanks. The effect of the amps used is central to the story but as far as I can see it is also nearly impossible to disentangle! (Even if we had McCartney’s amp…)
Kevin
Excellent, excellent job!!
Regarding McCartney’s D2 vs D3:
You may not be aware of this (if you don’t play guitar (or bass)), but if you pluck or pick a string in the right way in the right position, you can generate a note that is a mix of what the regular note sounds like and what the harmonic at that position sounds like.
For example: If you pick a guitar string at 1/4 the length of the string away from the bridge in the right way, you can get a nice 4th harmonic playing out of it. This technique can be heard on electric guitar riffs and solos in the 80s quite frequently.
So, one other contributing factor to McCartney’s sound is the way he plucked the string. If he plucked it at the midpoint (between bridge saddle and the fret his other hand was at) in the right way, it would elicit a very strong second harmonic for the D2, sounding like (and showing up as) a D3.
I have *no idea* if this actually happened; maybe nothing like this happened. But, ask your musician friend and brother about this, and see if they can replicate the plucked harmonic for you.
Hi,
Thanks, I wasn’t aware of that. It is certainly another possibility. Is there any reason why McCartney would have chosen to do that I wonder.
By the way, if you look at the transcribe picture of the D2, then you can see that the third peak is higher than the first. That is the third harmonic is louder than the first!
Kevin
Advanced guitar players do this, it’s second nature. There are also multiple ways to strum to get different sounds/harmonics.
Nice article.
Hi,
I have played with Randy Bachman for well over 13 years and was indeed part of the Guitarology Show you spoke of in your essay.
I also play in Revolver – The World’s Best Beatles Band (which is what Rick Neilson and Robin Zander of Cheap Trick called us when they came to one of our shows, and the title stuck)
My partner in the show Michael Sicoly and I, like Randy, are life-long Beatles fans so we have dissected this chord ad naseum (as well as all other Beatle nuances) and although what we did with Randy was very close, I agree with you that it’s still missing an X factor. (Not to mention that piano in the mix)
The chance that certain harmonics bled into the studio microphones that particular day that would never be simulated exactly the same again rings to be reasonably true to me. This is why artists sometimes grieve when they can’t capture the sound or performance from their demo recording when they go to record their song ‘for real’.
With that in mind, I must say that a musical ghost, if you will, can enter certain moments in performance and/or recording and, with its presence, the whole simply becomes bigger than the sum of its parts.
Thank you for all your hard and diligent analysis.
I value your work on this particular moment in musical history in very high regard.
Best,
Your Beatle pal Mick Dalla-Vee
Thanks Mick. You are probably right about it being greater than the sum of its parts!
Best wishes,
Kevin
Fascinating-I enjoyed the article as well and think the comments have been a nice compliment.
Great article, and great comments. I’m wondering if you’ve ever heard of the “Quintina”: in Sardinian vocal music, a male quartet will blend their voices in such a way as to create the illusion of a fifth, female voice. The fundamental and harmonics of the Quintina are created by blending the harmonics of the four male voices. This is highly speculative, but with the blending of instruments, the multiple strings of a single piano note, the interaction of instrument amplifiers and microphones, and who knows what else, its possible there’s one or more ghost notes in the original recording.
A bit of nit picking: An F chord with a G on top is not an augmented ninth. An augmented ninth is a G#, which would be very dissonant played over an F chord. Also, if you play the Fadd9 with the thumb, you place the thumb on the first fret, not the second. The second fret is F#, another dissonance if played with an F chord.
I’ve not previously heard of quintana, however barbershop singing also focuses on ringing chords in order to achieve this “fifth voice”.
It is probably unlikely, however, that different instruments could produce a sufficiently similar tone to create an audible overtone (it is difficult enough for singers with similar “instruments” to consistently match their voices).
Typo? Should R+L waveform read R+V?
“We ‘invert’ one waveform, L+V say, by turning it upside down, to get -L-V. We add this to the R+L waveform. What is the result?
The resulting waveform is R+V+(-L-V)=R-L.”
Yes! Corrected it. Thanks,
Kevin
… And if you do the other subtraction (-R-V)+L+V= L-R which you can add to the R-L you already have, to get just the left channel. You can also do it the other way round to extract the right channel.
Excellent work! The harmony resulting from all voices together could be described as a D minor eleventh (omit ninth). This expains why strumming an open guitar sounds similar as it is E minor eleventh, the same chord type one whole step higher. This is also very similar to D seventh suspended fourth, which does not include F but best describes what George Martin played. The sound could be played on a single six string guitar by detuning the lowest string one whole step, called Drop-D tuning. Strumming all six strings with the four string Fadd9 shape would give D2, A2, F3, A3, C4, G4. This only leaves out the G2 which could be achieved by detuning the A string, though it is impossible to simultaneously play both G2, and A2 on a single guitar (without additional detuning and omitting other notes). The next challenge would be to play the rest of the song in the altered tuning. This seems a daunting task for to non-guitarist like myself. Omitting the D2 and playing in standard tuning is perhaps the sensible choice thus giving the G7sus4: G2, A2, F3, A3, C4, G4.
I’m very late to this party, but I want to say that the solution suggested in the post above — that is, tuning the lower E string down to D and then playing 003213 — is EXACTLY the solution I came up with independently some time ago for playing the opening chord on a guitar. Nothing else in all the experimenting I did sounded more authentic that this.
I have to admit, this solution, at least for what the guitars play did leap out at me as I read the article.
Dropped D is probably the second-commonest tuning used by guitar players, and is especially common for acoustic playing.
Perhaps this is what Lennon played?
Re: the D2 vs D3 on the bass- you may very well have it with your supposition that the deeper bass register was rolled off in the mix. At least it would receive some backing from something written by Geoff Emerick (asst recording engineer then, later head Beatles engineer): EMI in the early 60s had a policy of attenuating bass frequencies, a rather archaic rule left over from the days when a heavy bass thump could cause the cutting lathe to jump! Emerick (and McCartney) chafed against this rule for some time, then just ignored it (beginning with Paperback Writer); but in 1964 it would be entirely plausible that George Martin pulled down the bass frequency fader, leaving the D3 overtone more prominent than the D2 fundamental.
Hi Bill,
Many thanks! That’s a useful piece of information. It helps build the case.
Kevin
this opening chord is without question the most iconic in popular music history…I always felt there was a piano in the mix, and was proven correct…exactly what notes are played is not as important as the “vibe” created by their combination, the attack, and the resonation after the fact…this produces the audial illusion that the ‘whole” is greater than the sum of the parts…the twangy effect of Harrison’s 12 string Rick and the vibration of the open piano strings also add a great deal of effect that may not necessarily be scientifically analyzable…the fascination behind the mysterious product these four lads were able to change the world with(as well as Martin) will continue to be a source of enlightenment and delight for many generations to come(speaking of vibe…maybe I even hear one on that chord??)
So true! More than the sum of its parts!
Kevin
Liked Your Post
Interesting that twice you use the phrase, “sum of its parts” – there is a podcast called Sum Of All Parts, and very recently they put up a discussion with Jason Brown of his work on The Chord.
It’s at http://www.abc.net.au/radionational/programs/sum-of-all-parts/6.0-magical-mystery-chord/9088624 and it would appear that he’s not convinced that he got it wrong.
Thanks! I’ll have to listen to that when I get home!
Kevin